Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
P1 - 3.
Considere una situación igual a la del problema anterior, pero suponga ahora que no hay fuerza de rozamiento sobre el bloque A de $20{,}0 \mathrm{N}$ que descansa sobre la mesa. La polea es ligera y sin fricción.
a) Calcule la tensión $T$ en la cuerda ligera que une los bloques.
a) Calcule la tensión $T$ en la cuerda ligera que une los bloques.
Respuesta
Si ahora no hay rozamiento, esta sería nuestra situación y claramente el sistema va a estar acelerado ¿no?
Reportar problema
*Aclaración: Si esto no te resultaba obvio, mirá el DCL del bloque A, en el eje $x$ únicamente tenemos a la tensión apuntando a la derecha... la sumatoria de fuerzas en $x$ claramente va a ser distinta de cero, así que la aceleración no podría ser cero ;)
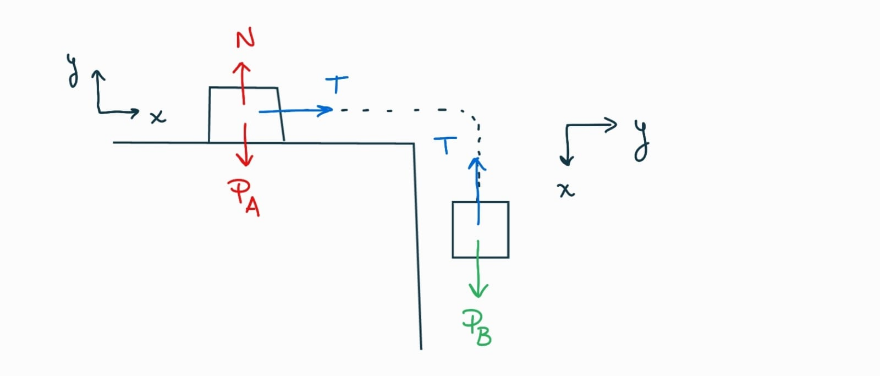

Antes de plantear segunda ley, averiguemos la masa de cada uno de los bloques
-> Bloque A
$P_A = m_a \cdot g$
$20 \text{ N} = m_a \cdot g$
$m_a = 2.0408... \text{ kg}$
-> Bloque B
$P_B = m_b \cdot g$
$12 \text{ N} = m_b \cdot g$
$m_b = 1.224... \text{ kg}$
Planteamos segunda ley para cada uno de los bloques:
Bloque A
$\sum F_x = m_a \cdot a$
$T = 2.0408 \text{ kg} \cdot a$
Bloque B
$\sum F_x = m_b \cdot a$
$P_B - T = m_b \cdot a$
$12 \text{ N} - T = 1.224 \text{ kg} \cdot a$
Perfecto, al igual que nos viene pasando siempre, tenemos un sistema de dos ecuaciones con dos incógnitas, $T$ y $a$
$\begin{cases} T = 2.0408 \text{ kg} \cdot a \\ 12 \text{ N} - T = 1.224 \text{ kg} \cdot a \end{cases}$
Resolviendo este sistema, deberías estar llegando a que...
$T = 7.50 \text{ N}$
y
$a = 3.68 \, \frac{m}{s^2}$
Bueno, en este ítem sólo nos pedían la tensión de la cuerda, genial, es $T = 7.50 \text{ N}$. Igualmente saber qué aceleración tiene el sistema nos va a servir para más adelante, guardate ese resultado ;)
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
